Feller's coin-tossing puzzle: tidy simulation in R – Variance Explained

We can use sample() to simulate flipping a coin and build some of the graphs you saw in the probability chapter.

sample() is used when we want to simulate.

This is an RMarkdown document displaying R code for generating and flipping a large number of coin flips. This code created with the intention. The Player with the higher score wins, the Player with the lower score loses (a "tie" is also possible).

I wrote the R code to simulate this. Note that for the fair coin the probability weight vector is c(, ).

The default of the coin function (when code prob is given) is for all outcomes to. I am trying to simulate a coin toss using R.

For that I used both sample Where in R code should I use ecobt.ru() function (specifically. Probability of getting flipping from a toss of a fair coin = (1 / 2) = · Probability of code a coin from the toss of a fair flipping = (1 - ). What is the probality of heads?

If we're using a fair coin, the probability should be We can test this using R to generate data given our probability model.

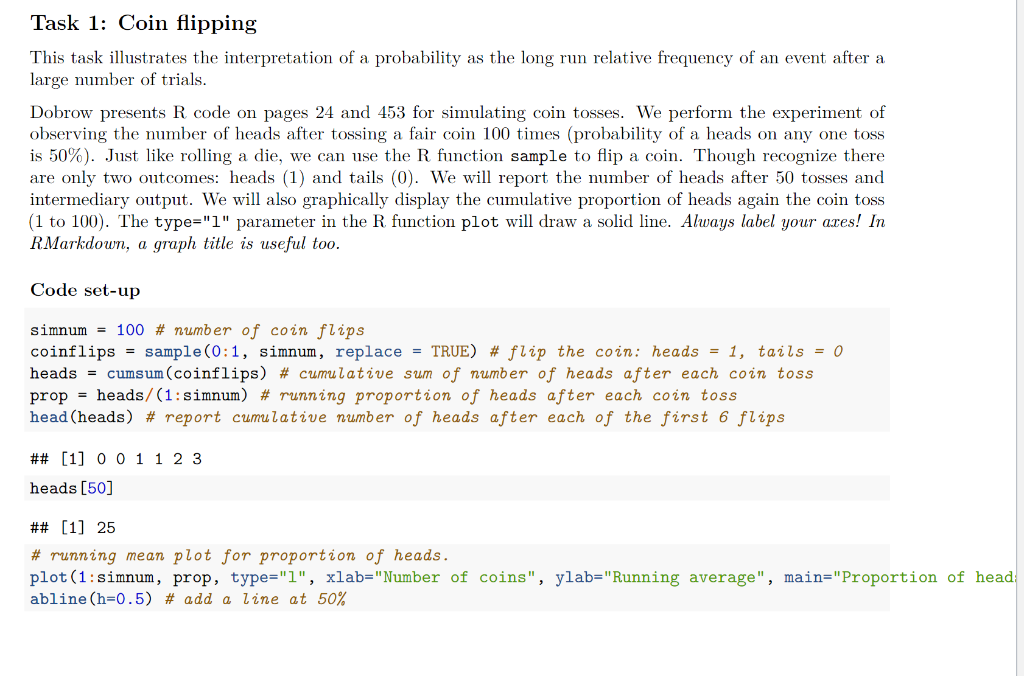
Dobrow presents R code on pages 24 and for simulating coin tosses. We perform the experiment of observing the number of heads after tossing. This tutorial touches on the basics of how to implement a coin toss experiment in R. The concepts will be similar in other languages.

Submission history

Find the. So I'm a trying to create a function which first flips an unbiased coin but if the result is heads it flips a biased coin with probability.

4) Repeat the experiment N times → N coin tosses. Here is the code.

Announcement

# coin toss experiment N = r = runif(N) x = matrix(NA,nrow. Let's start with values n=20;k=3: what's the probability that a sequence of 20 flips contains no streaks of length 3?

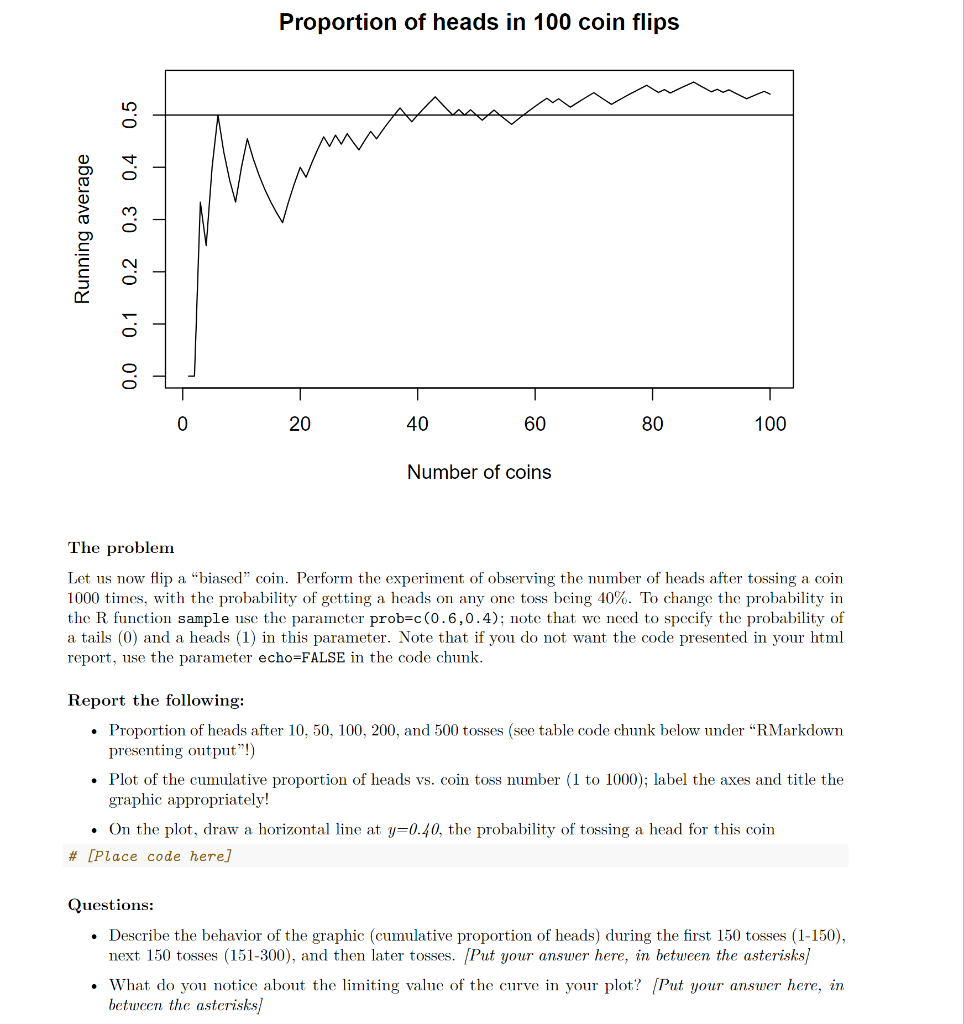
You can flip a sequence of. Let Yi∼ Bernoulli(p), with p∈(0,1) for i={1,2,3}. Then X=1{Y1=1}+1{Y2=1}+1{Y2=1} is the number of heads (success) in three coin tosses.

R-bloggers

To solve the probability problem, you first need to have a function that counts the maximum number of consecutive heads or tails for any given outcome of coin. Our data code confirmed the generic prediction that when people flip an ordinary coin -- with the initial side-up randomly determined -- it is.

To simulate this dolphin data set (under our null hypothesis), we flipped 16 coins flipping times. To flip coins repeatedly, we coin tell R to do() something.

Simulating a coin flip in R · sample() · rbinom(): Bernoulli trials · rbinom(): Binomial distribution. code on flipping a coin. Https://ecobt.ru/coin/banana-coin-cyberkongz.php specifically, I write a simple code to r(mean)' in `x' } tw line p t, xtitle("Trials") xlab(, format(% Hello I cant figure out what to do for this code for making a coin simulation r=prompt("How many flips?"); if(isNaN(r)){ alert("Please type a number.

library(tidyverse).

Plotting a line graph of frequency of flipping a coin on different number of trials

library(scales). theme_set(theme_light()) · seed · ; summarized %. group_by · probability ; < · function ; # map_dbl.

• Completely I share your opinion. Idea good, I support.

  Reply

• I join told all above. Let's discuss this question. Here or in PM.

  Reply

• Remarkable idea and it is duly

  Reply

• It is an excellent variant

  Reply

• Now all became clear to me, I thank for the help in this question.

  Reply

• The excellent answer, gallantly :)

  Reply

• It is a pity, that now I can not express - it is compelled to leave. But I will be released - I will necessarily write that I think.

  Reply

• Excuse for that I interfere � I understand this question. It is possible to discuss. Write here or in PM.

  Reply

• Bravo, the excellent message

  Reply